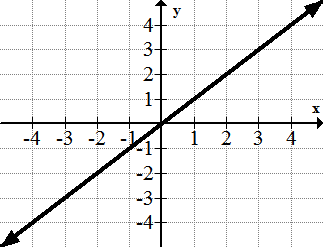Definition Of Identity Function With Example

But identity function can also be defined for the subset of the real numbers.

Definition of identity function with example. The identity function is a function which returns the same value which was used as its argument. Though this seems like a rather trivial concept it is useful and important. An inequality which is true for every value of the variable is called an identity inequality. The identity function on m is clearly an injective function as well as a.

But it is very common to use the equal sign. Identity functions behave in much the same way that 0 does with respect to addition or 1 does with respect to multiplication. We can consider sql scope identity function similar to the identity function but it is limited to a specific scope. In other words the function value f x in m that is the codomain is always the same input element x of m now considered as the domain.

X yf x xis an identity functionwe discuss more about graph of f x xin this postfind identity function offogandgoff. For example the linear function y 3x 2 breaks down into the identity function multiplied by the constant function y 3 then added to the constant function y 2. X xwe input xso we should get x gof xwe writegof ixwhe. X y g.

It is also called an identity relation or identity map or identity transformation if f is a function then identity relation for argument x is represented as f x x for all values of x. F x x for all elements x in m. An identity is an equation that is true for all values of the variables. The above equation is true for all possible values of x and y so it is called an identity.

Strictly speaking we should use the three bar sign to show it is an identity as shown below. F x x is an identity function. Identity function is a function which gives the same value as inputted examplef. In terms of relations and functions this function f.

In other words the identity function maps every element to itself. We use scope identity function to return the last identity value in a table under the current scope. Formally if m is a set the identity function f on m is defined to be that function with domain and codomain m which satisfies. Identity function definition is a function such as f x that is everywhere equal in value to the value of its independent variable such as x.

A function in which the domain values doesn t change at all. Conversely the identity function is a special case of all linear functions. A scope can be a module trigger function or a stored procedure. Y xgofgof g f x gof.

Here in case of the identity function the graph will be a straight line passing through the origin the straight line makes an angle 45 o with the x axis other examples of identity functions so far we observe the identity function for the whole set of real number.